![[Shownotes]](../gif/annotate/shide-51.gif)
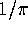 from the functions
from the functions 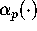 .
For a fixed initial value
.
For a fixed initial value 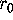 and a fixed p
we define the sequence
and a fixed p
we define the sequence 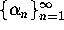 by
by

 Of course, as it stands, although it is clear that
Of course, as it stands, although it is clear that 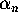 converges to
converges to 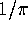 to p-th order, it is not very practical.
The idea is to write the sequence recursively. Therefore there are
two problems to solve:
Table 1 contains some functions we defined in MAPLE and that we
used to find and prove initial values and iterations.
to p-th order, it is not very practical.
The idea is to write the sequence recursively. Therefore there are
two problems to solve:
Table 1 contains some functions we defined in MAPLE and that we
used to find and prove initial values and iterations.


Our function etaq utilizes the expansion due to Euler:

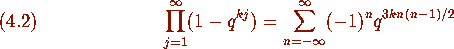 We are then able to effectively compute q-series expansions of
We are then able to effectively compute q-series expansions of 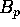 ,
, 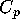 ,
,
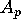 . We have written MAPLE procedures to compute all the necessary
functions.
. We have written MAPLE procedures to compute all the necessary
functions.