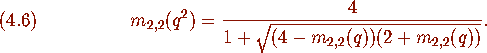![[Shownotes]](../gif/annotate/sshow-71.gif)
The problem is to find a recurrence relation for the 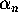 ,
defined in (4.1). An examination of (3.18) reveals that
we need to get
,
defined in (4.1). An examination of (3.18) reveals that
we need to get 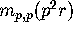 in terms of
in terms of 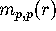 . From (3.14)
we see that this is equivalent to finding a relation between
. From (3.14)
we see that this is equivalent to finding a relation between 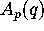 ,
,
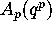 and
and 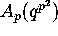 . Here we have written
. Here we have written 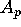 as a function of q
and not r. By using (3.15), it can be shown that
as a function of q
and not r. By using (3.15), it can be shown that 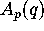 is
a
modular form
of weight two on a certain
congruence subgroup.
is
a
modular form
of weight two on a certain
congruence subgroup.
This implies
that all three functions 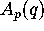 ,
,
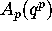 and
and 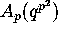 are
modular forms
of weight two on a certain
congruence subgroup
and hence must satisfy an algebraic relation of the form
are
modular forms
of weight two on a certain
congruence subgroup
and hence must satisfy an algebraic relation of the form

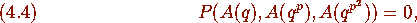 where P is a certain rational homogeneous polynomial of degree k, say.
The crucial observation is that the left-hand side of (4.4) is
a
modular form
of weight 2k.
It is well-known that
where P is a certain rational homogeneous polynomial of degree k, say.
The crucial observation is that the left-hand side of (4.4) is
a
modular form
of weight 2k.
It is well-known that
the dimension of the space of
modular forms
(above) of weight 2k is asymptotic to
some postive constant times k (see [10]). It is also well-known that
the number of monomials 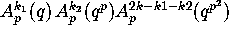 is
asymptotically equal to
is
asymptotically equal to 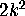 .
Hence there will always be a relation for large enough k.
Such a relation can be found and proved symbolically. This is really a
linear problem. The q-series expansion of each monomial up to
a certain power of q can be easily computed and stored as a column in a
matrix. Finding homogeneous relations is then equivalent to
finding the nullspace of a certain matrix. Such relations can be
proved by verifying them to a high enough power of q using the theory
of
modular forms
. See [7] for more details.
We illustrate the case p=2 with a
.
Hence there will always be a relation for large enough k.
Such a relation can be found and proved symbolically. This is really a
linear problem. The q-series expansion of each monomial up to
a certain power of q can be easily computed and stored as a column in a
matrix. Finding homogeneous relations is then equivalent to
finding the nullspace of a certain matrix. Such relations can be
proved by verifying them to a high enough power of q using the theory
of
modular forms
. See [7] for more details.
We illustrate the case p=2 with a
 MAPLE session.
MAPLE session.
> read funcs: > read findhom: > A2:=Aseries(2);

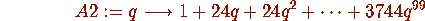 > findhom([A2(q),A2(q),A2(q)],2,100);
> findhom([A2(q),A2(q),A2(q)],2,100);
# of terms, 22
-----RELATIONS-----of order---,2

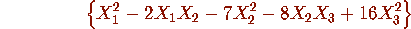 We now check the relations to O(q
We now check the relations to O(q t)
t)
---RELATION----, 1, ---checks to order---

 The function Aseries(2) gives the q-series expansion of
The function Aseries(2) gives the q-series expansion of 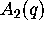 .
Using our function findhom we found that
.
Using our function findhom we found that 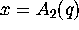 ,
, 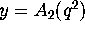 ,
,
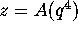 seem to satisfy the equation
seem to satisfy the equation

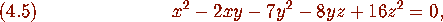 at least to
at least to 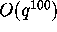 , which is enough for a proof.
By solving this equation we see that
, which is enough for a proof.
By solving this equation we see that