![[Shownotes]](../gif/annotate/shide-61.gif)
necessary MAPLE functions. > read funcs: > readlib(lattice):
> Digits := 30:
> alpha(7,1);

 > x:=":
> x:=":
> minpoly(x,2);

 > alpha(7,1/7);
> alpha(7,1/7);

 > x:=alpha(2,3);
> x:=alpha(2,3);

 > minpoly(x,4);
> minpoly(x,4);

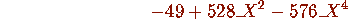 > solve(");
> solve(");

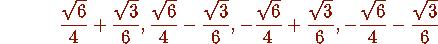 > evalf(alpha(2,3)-(3*sqrt(6)-2*sqrt(3))/12,100);
> evalf(alpha(2,3)-(3*sqrt(6)-2*sqrt(3))/12,100);


We have used MAPLE's implementation of the lattice algorithm []
The MAPLE function minpoly(x,n) finds a polynomial of degree n
with small integer coefficients satisfied by the real floating point
number x. The output depends on the number of digits computed
for the approximation x. In our session the function alpha(p,r)
corresponds to 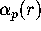 . Observe that we were able to verify
(3.10) and (3.20) for p=7.
We found a nice quartic polynomial which appears to be
satisfied by
. Observe that we were able to verify
(3.10) and (3.20) for p=7.
We found a nice quartic polynomial which appears to be
satisfied by 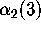 and that it appears that
and that it appears that

 Once we have such a conjectured value for
Once we have such a conjectured value for 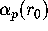 it is possible to prove the result by computing to enough
digits.
In this way we were able to find many initial values.
These are given in Table 2.
it is possible to prove the result by computing to enough
digits.
In this way we were able to find many initial values.
These are given in Table 2.