![[Shownotes]](../gif/annotate/shide-81.gif)
Once we have 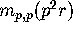 in terms of
in terms of 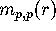 constructing
a p-th order iteration is a simple matter. We illustrate the
construction for p=2. We take
constructing
a p-th order iteration is a simple matter. We illustrate the
construction for p=2. We take 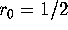 as our initial value.
We could have used any value from Table 2. We define two sequences
as our initial value.
We could have used any value from Table 2. We define two sequences
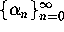 and
and 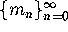 :
:

 Here we consider
Here we consider  as a function of r. From (3.19) and
(3.20) we have
as a function of r. From (3.19) and
(3.20) we have

 From (3.18) and (4.6) we have for
From (3.18) and (4.6) we have for 

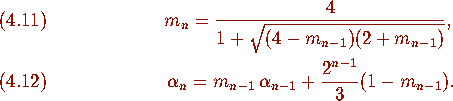 Equations (4.9)--(4.12) uniquely define the two
sequences
Equations (4.9)--(4.12) uniquely define the two
sequences 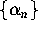 and
and 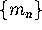 .
The convergence is quadratic. We illustrate with a MAPLE session.
> read iteration1:
> it1(5,100);
.
The convergence is quadratic. We illustrate with a MAPLE session.
> read iteration1:
> it1(5,100);

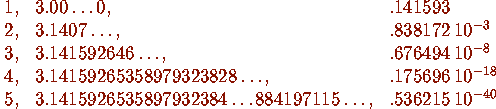 The function it1(5,100) computes the first 5 iterations to
100 digits and an approximation for the difference between
The function it1(5,100) computes the first 5 iterations to
100 digits and an approximation for the difference between
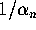 and
and  . We also note that this iteration is really
a known quadratic iteration [6, Iteration 3.6, p. 700,].
. We also note that this iteration is really
a known quadratic iteration [6, Iteration 3.6, p. 700,].