



Contents
Next: References
Up: Binary Cubic Forms and
Previous: Complex cubic fields
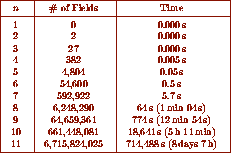
The following table gives the total number of real fields of discriminant up
to 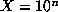 for
for 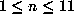 , as well as the elapsed time on a DEC Alpha.
, as well as the elapsed time on a DEC Alpha.

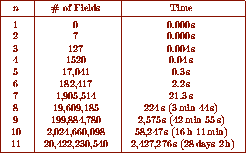
The following table gives the total number of complex fields of discriminant
greater or equal to to -X with 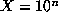 for
for 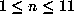 , as well as the
elapsed time on a DEC Alpha.
, as well as the
elapsed time on a DEC Alpha.

![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-91.gif)
It should be remarked that, thanks to the notion of reducedness, our algorithm
gives for every cubic field a canonical equation, which we can call
reduced, and which in addition has all the
nice properties described in Section 4. In particular the integral basis
and decomposition of primes is immediate. One consequence is that, when the
cubic number field does not have a power basis, the equation that we will
find will not be monic. On the other hand, if there exists a power basis,
the reduced equation produced by our algorithm is not necessarily monic.
We give a few examples.
- The cyclic number field with discriminant
961 can be given by the monic equation
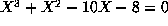 , but does not
have a power basis (an integral basis is
, but does not
have a power basis (an integral basis is 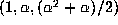 , where
, where  is a root of the above equation). Our algorithm finds the nonmonic reduced
equation
is a root of the above equation). Our algorithm finds the nonmonic reduced
equation 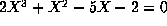 .
.
- The noncyclic number field of discriminant 1304 can be given by the
monic equation
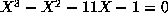 , but does not have a power basis
(an integral basis is
, but does not have a power basis
(an integral basis is 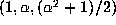 ). Our algorithm finds the nonmonic
reduced equation
). Our algorithm finds the nonmonic
reduced equation 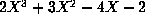 .
.
- The noncyclic number field of discriminant 2228 can be given by the
monic equation
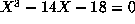 , and this times it has a power basis. On the
other hand our algorithm finds the nonmonic reduced equation
, and this times it has a power basis. On the
other hand our algorithm finds the nonmonic reduced equation
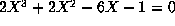 .
.


Contents
Next: References
Up: Binary Cubic Forms and
Previous: Complex cubic fields
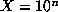 for
for 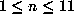 , as well as the elapsed time on a DEC Alpha.
, as well as the elapsed time on a DEC Alpha.
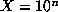 for
for 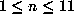 , as well as the elapsed time on a DEC Alpha.
, as well as the elapsed time on a DEC Alpha.
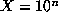 for
for 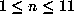 , as well as the
elapsed time on a DEC Alpha.
, as well as the
elapsed time on a DEC Alpha.
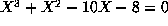 , but does not
have a power basis (an integral basis is
, but does not
have a power basis (an integral basis is 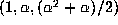 , where
, where  is a root of the above equation). Our algorithm finds the nonmonic reduced
equation
is a root of the above equation). Our algorithm finds the nonmonic reduced
equation 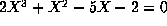 .
.
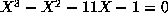 , but does not have a power basis
(an integral basis is
, but does not have a power basis
(an integral basis is 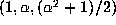 ). Our algorithm finds the nonmonic
reduced equation
). Our algorithm finds the nonmonic
reduced equation 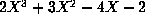 .
.
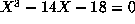 , and this times it has a power basis. On the
other hand our algorithm finds the nonmonic reduced equation
, and this times it has a power basis. On the
other hand our algorithm finds the nonmonic reduced equation
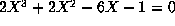 .
.