![[Shownotes]](../gif/annotate/shide-71.gif)


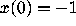 and various values for
and various values for 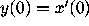 .
.
It is easy to
see that there is no oscillatory behavior, but are there any solutions
that are bounded? An interesting computer exercise for the student is
to try varying the initial values for the velocity 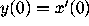 ,
while holding
,
while holding 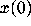 fixed, in order to find an experimental value for
fixed, in order to find an experimental value for
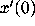 that gives a bounded solution. (We selected
that gives a bounded solution. (We selected 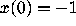 to make
the experiment more interesting, since
to make
the experiment more interesting, since 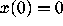 gives the trivial
solution.) Our computer experiments indicate that if
gives the trivial
solution.) Our computer experiments indicate that if 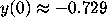 , the solution appears to remain bounded as t becomes large
negative.
To find out what is really going on, we turn to the Riccati equation
associated with the Airy equation
, the solution appears to remain bounded as t becomes large
negative.
To find out what is really going on, we turn to the Riccati equation
associated with the Airy equation 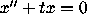 .
.